Interest in Crypto investing is at an all time high. As of this writing the entire cryptocurrency market capitalization is valued at over $1 Trillion USD with thousands making their first investment every day. Cryptocurrencies and blockchain technology have been an area of interest of mine for close to a decade. With all the newcomers to the space and it’s domination in the news cycle the question always gets asked “What cryptocurrency should I invest in?” The short answer for about five years has been more or less “Mostly Bitcoin and Ethereum, but look into [insert new hot project here]” The thesis being Bitcoin and Ethereum are two projects that will stand the test of time but you should expose a percentage of your portfolio to new emerging projects. While it’s clear that this has worked let’s see if the data backs this up.
First and foremost, we must select a collection of cryptocurrencies to test this with. I stuck with coins in the top 50 of market capitalization, have been through at least one previous market cycle (this meant coins quality and highly performing coins like Cardano’s ADA, Chainlink, Binance’s BNB, Polkadot, and others could not be included due to lack of historical data), and I didn’t include “meme coins” like Dogecoin due it’s appreciation being more in part to anomalies than providing meaningful utility. I ended up choosing Bitcoin, Ethereum, Ripple’s XRP, Litecoin, and Stellar Lumens for this test.
To find the “best” portfolio we need to apply a mathematical model to the historical price data. There’s no perfect model but I’ve applied Modern Portfolio Theory to the data set. Historical price data is pulled from the coingecko.com API due to it being free and easy to work with. Modern Portfolio Theory was introduced by Nobel Prize winning economist Harry Markowitz. MPT doesn't look at a given asset's risk-return but rather how that one asset effects the entire portfolio's risk-return. This allows one to construct a portfolio with the biggest return given an accepted level of risk. An additional metric to examine is the Sharpe Ratio. The Sharpe Ratio was made by William Sharpe and assigns a number to a portfolio give it's return subtracted by the risk free rate, divided by the standard deviation of the portfolio's excess return. In short, a high Sharpe Ratio will give a better return than a portfolio with a smaller Sharpe Ratio. Using these two we can see what would be in theory the optimal portfolio.
What did we find? In the portfolio with the high Sharpe Ratio the breakdown is as follows.
| Bitcoin | Ethereum | Ripple | Litecoin | Stellar |
|---|---|---|---|---|
| 40.08% | 28.32% | 0.62% | 11.16% | 19.81% |
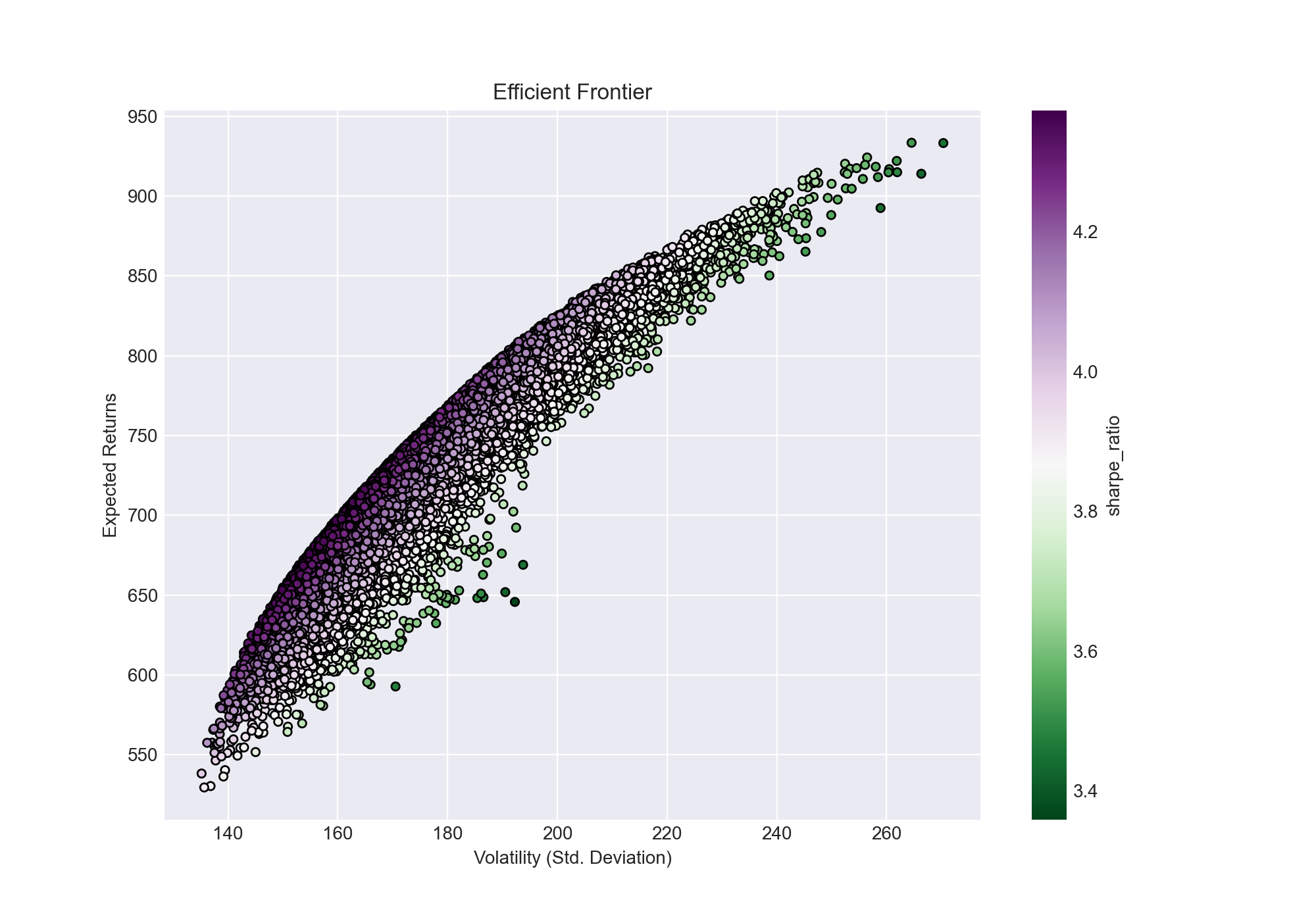
The portfolio above is the highest performing data point on the graph above. 68% of the portfolio is allocated to Bitcoin and Ethereum. One reason for this is their strong growth for the past 4 years and perhaps more importantly, their relative lack of volatility. While both BTC and ETH have both experienced 1 year drops of 80%+ that is not as great as the 90%+ drops many altcoins have experienced. When optimizing your portfolio, one lying on the efficient frontier represents the combination offering the best possible expected return for a given risk level, you take into account both returns and the downside risk. One thing I found surprising was the low percentage of XRP. XRP has a massive following with many investors excited about their future and it does reflect XRP’s general price instability.
What does this mean for the new crypto investor? Bitcoin and Ethereum should comprise the majority of one's portfolio. Many coins and tokens can have massive gains and a $5 price per token looks much more enticing than Bitcoin’s current $40,000 price but the data speaks for itself.
For as long as I can remember I’ve been a big fan of basketball. I enjoy playing basketball, watching basketball, and following and debating the NBA. One of the biggest conversations in basketball is comparing different players to each other and who should be awarded certain accolades. This most prestigious of which in the NBA is the Most Valuable Player award. This is awarded to whom the voters deem as, you guessed it, the most valuable player in the league. Growing up when debating one player over another I would always use stats to back up my arguments. So when I decided to take the wealth of historical NBA data and see if I can use a machine learning model to accurately predict which players would win the MVP award.
The first challenge I ran into was determining how to decide if a player wins or not. Looking deeper into the process for determining MVP I saw that 121 selected voters were to assign players votes ranging from first place (most valuable) to fifth place (fifth most valuable). Historically, it comes down to who gets the most first place votes. There hasn’t been an instance of a player winning the award from getting a lot of 2nd place votes. So I decided to predict the amount of first place votes a player would get.
The next challenge I faced was which statistics I would use to predict the number of votes. Using basketball-reference.com to collect the stats, I took every player that received votes for MVP in the past 10 years and recorded their advanced statistics. I chose advanced statistics because they can give a better indication on a player’s performance and impact on the game. In addition to this I didn’t base predictions on the players’ raw stats rather I chose their rank in the league for the year. Reason being, the MVP award is given to the most valuable player for that year. Just using the raw numbers would have the model make predictions based on every players performance in the history of the league rather than against the performances of other players from that season. Doing this I had the necessary to make predictions. After performing a feature selection I decided on using three different statistics: PER (Player Efficiency Rating), VORP (Value Over Replacement Player), and WS (Win Shares). PER was a statistic made by John Holligner which “sums up all a player’s positive accomplishments, subtracts the negative accomplishments, and returns a aper-minute rating of a player’s performance.” As per Basketball-Reference.com, VORP is “an estimate of each player’s overall contribution to the team, measured vs. what a theoretical “replacement player” would provide.” The top 10 seasons all time for VORP is a list populated by Michael Jordan, LeBron James, David Robinson, and Chris Paul, all players who have finished at least top two in MVP voting. Basketball-Reference.com defines Win Shares as “Win Shares is a player statistic which attempts to divvy up credit for team success to the individuals on the team.” With all of these stats available I was ready to begin doing some analysis.
When choosing an algorithm to predict a player’s received votes I chose to a regression algorithm rather than a classification because the number of votes received is a continuous numerical result rather than a discrete one that would be better suited for a classifier. I began with a simple Linear Regression.
A simple Linear Regression posed two problems for this data set. One was that the algorithm only accepted a single input variable where I had many and two it had rather mediocre performance. With a Root Mean Squared Error of 11.87 I knew it was possible to get better performance. In an attempt to better utilize the data I decided to use a multi-dimensional Linear Regression. This algorithm works similar to the previously used one however it uses multiple input variables. Using all three input variables rather than one I got a slightly better Root Mean Squared Error.
The weakness of Linear Regression in this application is the data used isn’t linear as demonstrated by this graph of Votes and PER
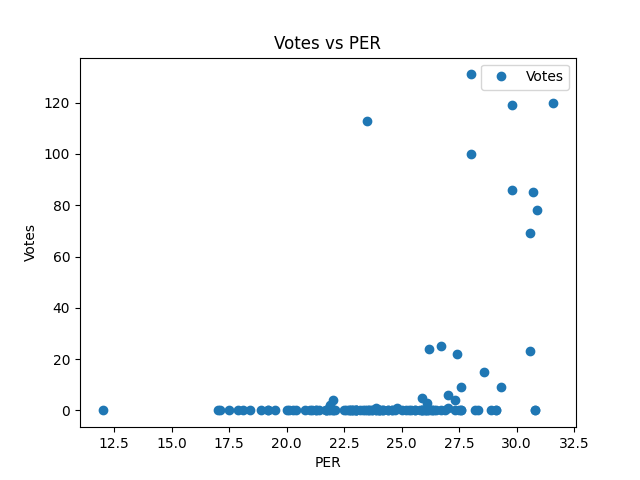
Because of this I then decided to go with a good algorithm for non-linear data sets: a random-forest regressor. The way how random-forest works is by creating a number of decision trees and using the mean of the trees to predict the outcome. Random Forest works for this application because it is a non-linear model. When running a random forest I got an error of 3.46 votes which was far better than what I got with a linear regression. To test how it compared to real life MVP voting I had the model predict who won in 2017, a highly contested year where many people were split between James Harden and Russell Westbrook. The model said Westbrook should have received 79 votes, more than the 69 votes he received in real life.
Application of historical data to modern basketball is both interesting and controversial. While in my opinion analytics can be very telling to gauge a player's performance some neglect the "eye test" and intangibles that makes a player great. There are some advanced statistics that translate well between between different eras of the game that quantify player performance and their contributions to a team's success and will stand the test of time as indicators. Ways to improve this could acquiring more data (a decade of MVP voting was used in this test), using different sampling methods, or using different stats such as those quantifying team performance. Revisiting later for other awards and future awards may yield interesting results.